In March 2012 Mike, a high school teacher in New York, pointed out an error on this page.
It has been corrected.
Thanks Mike.

Hi Tom,

The quick answer is it depends on the stadium and the conditions. Using some basic Physics equations, we can figure out how high and far the ball can travel under ideal conditions. You would need to know the horizontal distance from home plate to the edge of the opening of the stadium and also height from the field. Here are the assumptions I am making:

• path is parabolic
  
  
• velocity of 110mph or 49.17 m/s. The top velocity recorded of a baseball leaving a bat is about 110 miles per hour which is about 49.17 meters per second.
  
  
• the ball is hit at a 45 degree angle (to maximize the horizontal distance). If you increase the angle, it will increase the maximum height the ball reaches but it will decrease the horizontal distance form the plate.
  
  
• the ball is hit from a height of 0 m. This will make the calculations simpler and will not change the answer by very much.
  
  
• ignoring wind or any other outside factors that may change the path of the ball

Since the path of the ball is at an angle, we need to break down the initial velocity into horizontal velocity and vertical velocity.

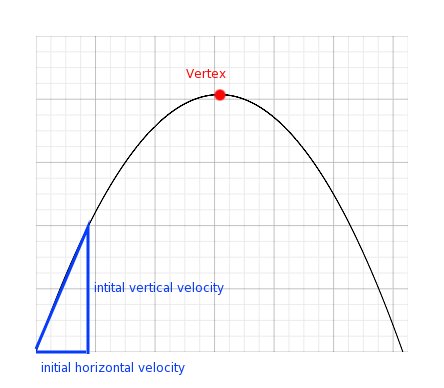
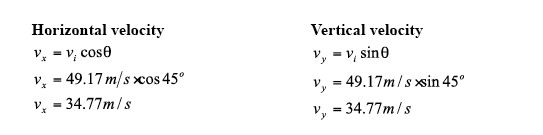
We know that acceleration due to gravity is -9.81m/s/s (it will slow down the vertical velocity). The vertical velocity as the hits the ground will be the same velocity but opposite sign of the initial vertical velocity. We can use these facts to determine the total time the ball will travel (if uninterrupted). Since the path is assumed to be parabolic, the maximum height (the vertex) is half the time of the total time.

Time

$v_f = v_i + at$

$v_f - v_i = at$

$\large \frac{ v_f - v_i }{a} = t$

$\large \frac{ -34.77 m/s-34.77 m/s }{-9.81 m/s^2} =\normalsize t$

$t = 7.09 s$

From the initial velocities, time when the height is at the maximum and acceleration due to gravity, we can determine the maximum height of the path (the vertex). At the vertex $t = \large \frac{7.09}{2} \normalsize = 3.54 \; s.$

Now that we know the vertex, we can find the equation of the parabolic path. From the equation of the parabola, we can find the height of the ball at 320 ft (the distance to the right back wall).

Equation of the path of the baseball (parabolic)
Vertex $(123.09, 61.62)$
Home base $(0, 0)$

General equation of a parabola with vertex $(p, q)$
$ y = a(x - p)^2 + q$

The parabola passes through $(0, 0)$ and hence

$0 = a(0 - 123.09)^2 + 61.62$

$-61.62 = 15193.03 a$

$a = -0.0041$

and thus

$y = -0.0041 (x - 123.09)^2 + 61.62$

We can now find the height of the baseball at $320 ft \approx 97.54 m,$ the distance to the back fence.

$y = -0.0041 (97.54 - 123.09)^2 + 61.62$ s

$y = 58.94 m \approx 193 ft$

Hope this answers your question,
Janice with help from Mike