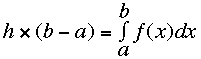Hi Vern,

For a function y = f(x) whose graph is above the x-axis on the interval [a, b], the average value of the function on the interval from a to b is the height h so that the area under the graph of y = f(x) from a to b is the same as the area of the rectangle with base [a, b] and height h.

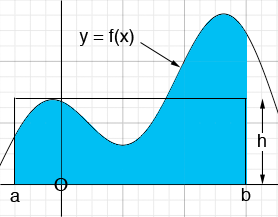
That is the average of the function y = f(x) from a to b is the number h so that

In your example yo want the average value of the rate of change of f(x) which is the derivative of f(x) so differentiate f(x) = sin(x) to obtain f '(x) = cos(x) and apply the definition of the average value to the function f '(x) = cos(x).

Harley