Hi Vi,

You can approach this problem using the binomial distribution but I prefer to describe it using a tree diagram.

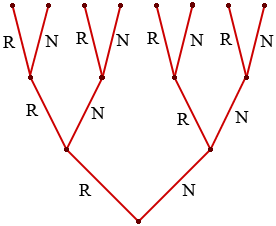
Each level in the tree represents the response from a customer, R if their oven needs repair and N if it does not need repair. If the manufacturer is correct then the first customer responds with R or N with probabilities 0.1 and 0.9 respectively. Regardless of the response from the first customer the second customer can respond with R or N again with probabilities 0.1 and 0.9, and likewise for the third customer.

Each path through the tree from bottom to top then represents a possible sequence of responses. For example the path RRR represents three rejections and the probability that you receive this response is 0.1 × 0.1 ×0.1 = 0.001. Now look for paths through the tree with two Rs and one N. There are three such paths, RRN, RNR and NRR. Each of these paths has an associated probability of 0.1 × 0.1 × 0.9 = 0.009. Thus the probability that the responses from the three customers contain exactly 2 rs is 3 × 0.009 = 0.027.

Thus the probability that at least two of the three ovens will need repair in the first year is 0.001 + 0.027 = 0.028.

Harley