Hi Jenina,

You need to think of the question in terms of distance and time:

- How much time passes while the distance between the two cars is increasing?

- How much time passes while the distance between the two cars is decreasing?

While there is increasing distance between the cars, the police car is speeding up from 95km/h (26.4m/s) to 145km/h (40.3m/s). Once the police car is traveling faster than 40.3 m/s, the distance between the two cars will begin to decrease. It is fairly simple finding when the police car to reach a speed of 40.3m/s using the formula:
v_f=v_i+a(t₂-t₁) where v_f=40.3m/s, v_i=26.4m/s, a=2.00 m/s² and t₁=1s

The formula yields t₂=7.94s
(or Δt=6.94s, how long it takes for the police car to reach 40.3m/s).

Next we need to consider how much time passes while the distance decreases between the two cars. Since we do not know the final speed of the police car when it overtakes the speeder, we need to consider the distance driven as it relates to time. Consider the following equivalent statements:
distance driven by speeder = distance driven by police car
distance while driving faster than police + distance while driving slower than police = distance while driving slower than speeder + distance while driving faster than speeder
distance while driving faster than police at constant speed+ distance while driving slower than police at constant speed= distance while driving slower than speeder at constant speed+distance while driving slower than speeder with acceleration+ distance while driving faster than speeder with acceleration

The last statement results in the following equation:

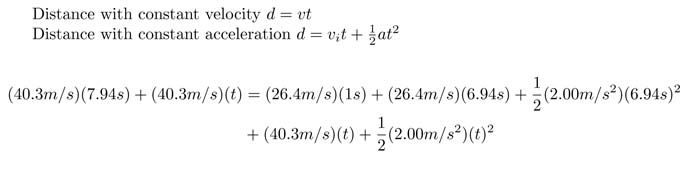
Solve for t and will know how much time passes while the distance between the two cars decreases. Add the two times together and you will know how long it takes the police car to over take the speeder.

Hope this helps. Bare in mind that there is more than one way to approach this problem.

Janice