Hi Katie,

First step in determining if y is a function of x or not, is isolating y. For example, say you are given x²+y²=4

y²=4-x²

y=±√4-x²

Next step is graphing. Draw a series of vertical lines. If any of these vertical lines goes through the graph more than once, it is not a function. If each vertical line goes through the graph only once, it is a function.

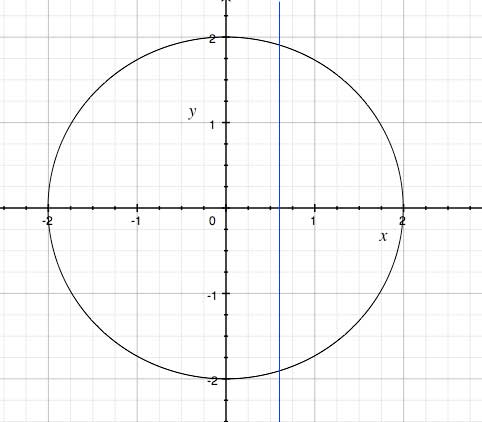
Clearly the vertical line goes through the graph more than once so this is not a function.

On the other hand, say you are given xy-3y-x=0

xy-3y=x

y(x-3)=x

y=x/(x-3)

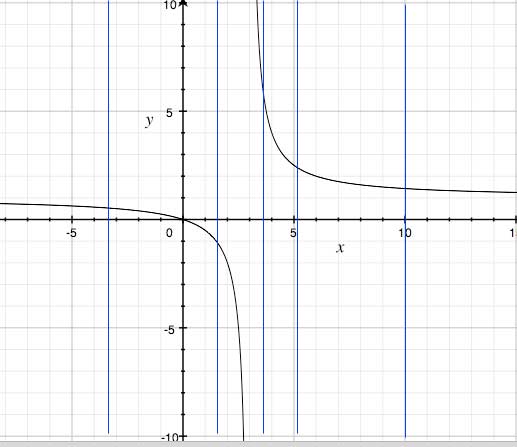
Looking at the graph, the vertical line crosses the graph only one time so y is a function of x. The definition of a function is for every value of x there is only one y value, that is why the vertical line test works. This graph in particular is a rational function because of the fraction.

Hope this helps,

Janice