| |||
| Math Central | Quandaries & Queries |
|
lanny, a student: a triangular trough is 10 feet long, 6 feet across the top, and 3 feet deep. if water flows at the rate of 12 cubic inches per minute, find how fast the surface is rising when the water is 6 inches deep. |
Hi Lanny,
I assume from the information you gave, the trough looks like this:
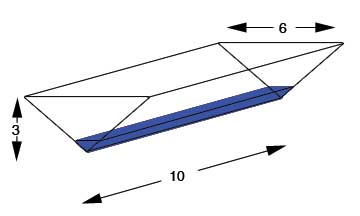
The volume of the triangular prism is area of the triangle x the length or V=1/2 bhl. Notice that the base of the triangle is twice as big as the height so we could simplify the formula for volume to V=1/2 (2 h)hl=h2l. Also remember that l is constant when the trough is filling so we can substitute 10 feet right into the formula so V=5h2. Lastly, use implicit differentiation to solve for your rate of change but don't forget to make sure all of the units of measurement are the same.
Hope this helps,
Janice
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.