Hi Michelle,

I find it is easiest to determine domain and range by looking at the graph of the function.

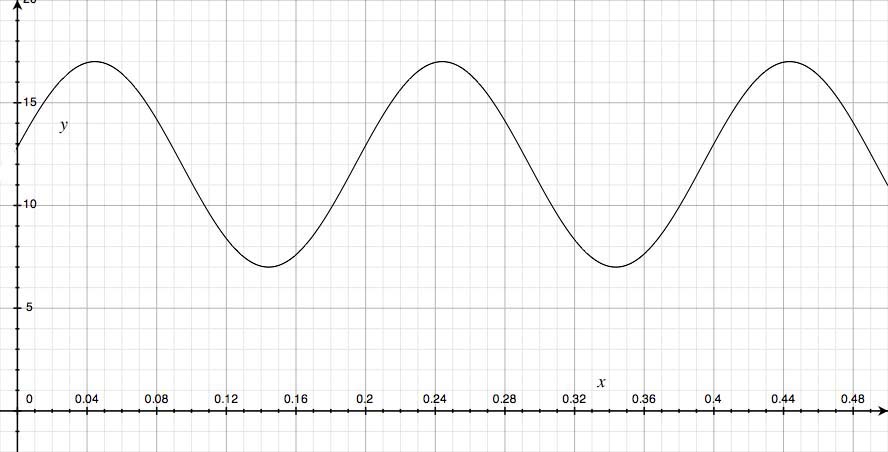
Remember that since the number of months cannot be negative, the domain is n≥0. Normally the domain of a sine function is all real numbers.

We can see from the graph that the range of function is 7≤w≤17 but can also find it the range just by looking at the given equation. As it is written, w=5sin(31.5n+63) +12 is very close to being in standard form which is useful for graphing and determining the properties of the function. Standard graphing form of a quadratic function is y=a sin b(x-c)+d where a is the amplitude (height of a wave), b gives use information about the period (how often it repeats), c is the horizontal shift and d is the horizontal shift. From standard graphing form, range is d-a≤x≤d+a.

Hope this helps,

Janice