Hi Ram,

Since AD and PM are both medians, we know that BD=DC, QM=MR. If D is the midpoint of BC then draw FD parallel to AC and ED parallel to AB. Join EF. I'll just refer to ΔABC but the same steps apply to ΔPQR.

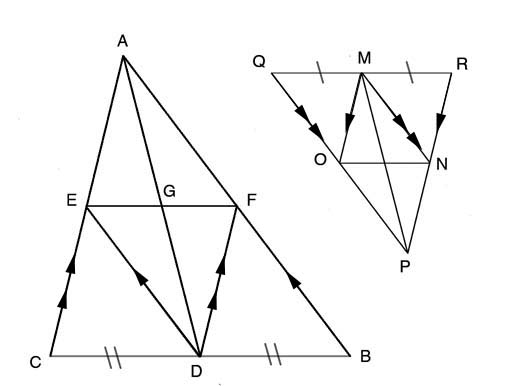
∠FBD=∠EDC & ∠FDB=∠ECD because they are corresponding angles with the parallel lines. ∠CED=∠DEF are also congruent because if two sets of angles in triangle are congruent then the remaining angles are also congruent. Since CD=DB then ΔBFD is congruent to ΔDEC.

∠CED=∠EDF because they are alternate interior angles of parallel lines. EC=FD and FB=ED since they are corresponding parts of congruent triangles and as a result then ΔEDF is congruent to ΔDEC.

By substitution we know that ΔBFD is congruent toΔEDF so then their corresponding angles, ∠DEF & ∠EDC and ∠DFE & ∠ECD are congruent. ∠AFE = ∠ DEF and ∠AEF=∠EFD because are alternate interior angles with the parallel lines. Since EF=EF then ΔAFE is congruent to ΔDEF as well as ΔDEC & ΔBFD by substitution. So we know that ∠EAF = ∠FDE, AF=FB, AE=EC in addition to CD=DB. This means that 1/2 AB=BF=AF, 1/2 BC= BD=CD and 1/2 AC=AE=EC so ΔABC is similar to each of the smaller triangles.

Within ΔABC, a parallelogram AFDE is formed. Since we are given that AC is proportional to PR, AB is proportional to PQ and AD is proportional to PM, we know that AF is proportional to PO and AE is proportional to PN. Since opposite sides of a parallelogram are congruent then DF is proportional to MN and DE is proportional to MO also, this makes parallelogram AFDE similar to parallelogram POMN. Now we know that ∠CAB=∠RPQ thus proving that ΔABC is similar to ΔPQR since the two proportional sides and the included congruent angle makes the triangles equiangular.

I know this is a lot of information but I hope this helps,

Janice