All irregular polygons do not have a circle that is tangent to each side, the exception is the triangle. If you were to draw a polygon at random, it is unlikely that there is a circle that has every side as a tangent. Irregular polygons do not have a centre but rather a centroid which is the arithmetic mean of each of the coordinate points. For a convex irregular polygon, the centroid lies within the polygon and for a non-convex polygon the centroid lies outside the polygon. If you find the centroid of a irregular, this would be your best bet for finding a circle that cuts all sides of a irregular. Even though it is slightly more likely that you could find a circle that can cut or be tangent to the sides a an irregular polygon, there are still polygons that it would not be possible for a circle to touch all sides. Consider the polygon below:

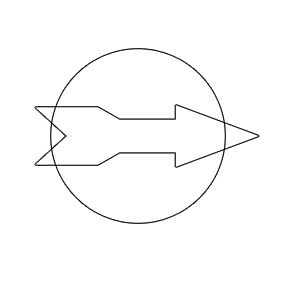
There is no size or position I could put a circle that would touch all sides of the polygon. You can however start with the circle and draw the irregular polygon around it.

Hope this helps,

Janice