Hi Adrian. I started by drawing the diagram, assuming the square shared the vertex Q with the triangle, and then I labelled the other corners of the inscribed square. I called the length of the square x, and used that to determine the other lengths.

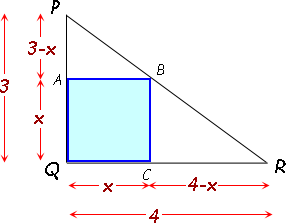
Let's consider the areas of the shapes. The large triangle PQR is composed of two right triangles PAB and BCR as well as the square. So if you add the areas of these three shapes, you get the area of the large triangle:

Area(PQR) = Area(PAB) + Area(BCR) + Area(AQCB)

Since we know that the area of a triangle is half the base times the height and the area of a square is the side squared, this makes:

(½)(4)(3) = (½)(x)(3 - x) + (½)(4 - x)(x) + x² .

Solve for x.

Cheers,
Stephen La Rocque.