Hi Bill.

A difference of cubes is of course a perfect cube minus a perfect cube.

I assume your student already has the formula

a³ - b³ = (a - b)(a² + ab + b²)

We can prove this using polynomial division.

First, we look at the roots of a³ - b³ and immediately we can see that if a = b, then a³ - b³ = 0, so (a-b) is a factor.

Next, rewrite it: a³ - b³ = a³ + 0a²b + 0ab² - b³ and use synthetic (or long) division to find the other factor. I'll use long division:

You could do something very similar for a sum of cubes.

However, there is a geometric way of seeing this too, at least where a and b are positive and a > b:

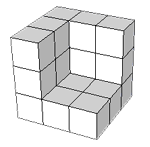
For example, say a= 4 and b = 2. Here is 4³ - 2³:

and here is 3³ - 2³ :

Let's take apart 3³ - 2³ first. The red object is broken into the other colours:

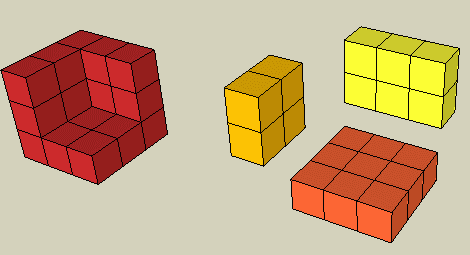
So the red object is composed of the orange piece which is 3² plus the yellow piece which is 3x2 and the gold piece which is 2². So the original 3³ - 1³ equals the components 3² + 3x2 + 2². Now since (3-2) = 1, we can multiply by this and not change anything, so we've shown

3³ - 2³ = (3-2) (3² + 3x2 + 2²)

But what about trying something harder, like 5³ - 2³?

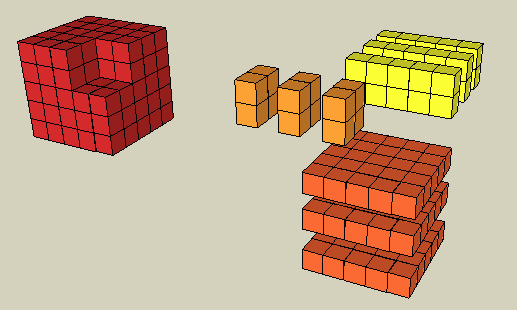
We have the same breakdown, but there are 3 copies of everything! This makes sense because (5-2) = 3.

So we've shown that

5³ - 2³ = (5-2) (5² + 5x2 + 2²)

just as the formula predicted and our long division proved algebraically.

If you look carefully at the last diagram, you can consider it as a³ - b³ and show that the number of copies is always (a-b), thus proving the general case.

I'd encourage your student to explore in this way the sum of cubes and see if she can come up with a similar algebraic and geometric solution.

Cheers,
Stephen La Rocque.