| |||
| Math Central | Quandaries & Queries |
|
Question from Bruce, a teacher: I have been trying to find a formula that relates height of a segment from the bottommost point of a circle toward the center of the circle to the corresponding distance along the circumference of the circle (i.e. at the point on the circumference intersected by a line perpendicular to that segment). The unknown variable is the height of the segment; the known variables are the radius of the circle and the distance along the circumference. Thank you |
Hi Bruce. I always start geometry problems with a diagram, adding variables and extra lines as I go:
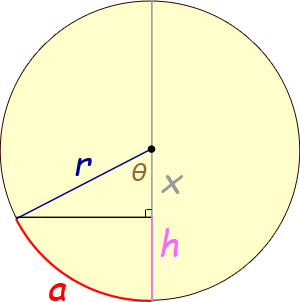
There are two key ideas here:
1. The relationship between the radius, the arc length and the central angle (when measured in radians) is: a = rθ.
2. The top triangle is a right triangle, so knowing r and θ permits you to find x using cosine.
Since h = r - x, that's the last piece of the puzzle. Thus,
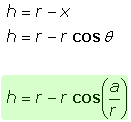
Just remember to use radians rather than degrees for the angle in the cosine. Alternatively, convert to degrees by multiplying a/r by π/180.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.