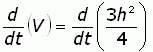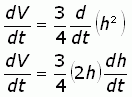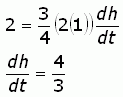Hi Christina.

You have a rate of change of volume and want to know the corresponding rate of change of depth at a particular depth.

This problem can be solved in three steps:

1. The first step is to find an equation that relates water depth to volume.
2. The second step is to take the derivative of both sides of the equation with respect to time.
3. The final step is to substitute in the values you are given for the depth and the rate of volume change and you will get the rate of depth change, that's the answer to the problem.

Here's how to do this:

1. Find the equation

The volume of the water in the trough equals the length of the trough times the cross-sectional area of the trough up to the depth it is filled with water. The cross section is an isosceles triangle, of course, whose shape is defined by the relative sizes of its sides (these are given). The length is constant.

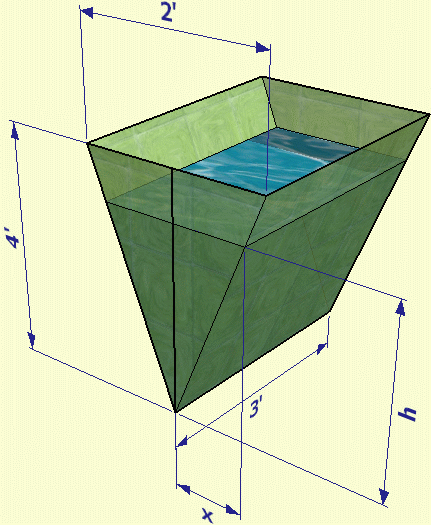The area of the isoceles triangle filled with water is xh. Can you see why?

We can use the principle of similar triangles to relate x to h though:

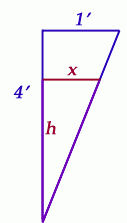
The ratios of corresponding sides of similar triangles are equal. So

So if we know h, we know x (and vice versa).

Since the area of the isosceles triangle is xh, this equals (h/4)h = h²/4. And because the volume of water (V) is equal to this cross-sectional area times the length of the trough, then we have an equation relating the volume of water to the depth (h) of water:

2. Take the derivative of the equation with respect to time.

To do this derivation, we have to use the chain rule on the right hand side:

3. Substitute known values and solve.

We know that the change in volume with respect to time is 2 cubic feet per minute. That's dV/dt (the change in volume over the change in time). We also know that we are interested in the value dh/dt, the change in height (water depth) over the change in time. That's what we want to find. And finally, we know that we are interested in the point where the depth of the water (h) is 1 foot. So we substitute a 2 for dV/dt and a 1 for h, and then solve for dh/dt:

Therefore, the surface is rising by 4/3 meters per minute when the water is 1 foot deep.

Cheers,
Stephen La Rocque.