 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Question from Courtney, a student: hey, how would i find the area of a quadrilateral.. need help desperately!! the sides are a (/) is 6cm b (_) is 9 cm and c (\) is 7 cm.. the angle between a and b is 140 degrees and b and c is 115 degrees.. the bottom/ side d is longer than the others and is unknown as are the bottome 2 angles! DO NOT KNOW HOW TO DO IT!!!!! PLEASE HELP! |
Fear not, Courtney! This is a job for the Law of Cosines.
I'll show you how it is done with a similar geometry and you can apply the same steps for your question:
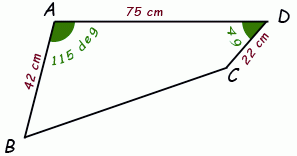
Here we know three lengths: 42, 75 and 22 and two angles: 115° and 49°.
We want to discover the area of the quadrilateral.
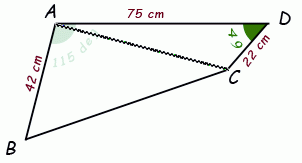We begin by constructing a line between A and C. Now we have divided the quadrilateral into two triangles. The sum of the areas of the two triangles is, of course, the area of the quadrilateral.
If we can discover two lengths and an included angle for each triangle, we can use the Area = ½xy Sin Z area equation to calculate the areas of the triangles.
We need to know the length of segment AC for the bottom triangle and we can use the Law of Cosines on the top triangle to give us that:
| AC2 = | DC2 + AD2 - 2(DC)(AD)Cos(CDA) |
| = | 222 + 752 - 2(22)(75)Cos(49°) |
| AC = | 62.8. |
We need the included angle CAB between AC and AB in order to find the area of the lower triangle. We know angle DAB is 115°, so if we can discover angle DAC, we can subtract and find angle CAB. Again, we can use the Law of Cosines on the upper triangle:
| CD2 = | AD2 + AC2 - 2(AD)(AC)Cos(DAC) |
| 222 = | 752 + 62.82 - 2(75)(62.8)Cos(DAC) |
| Cos(DAC) = | 0.9644 |
| DAC = | 15.33°. |
Thus, angle CAB = 115 - 15.33 = 99.67°.
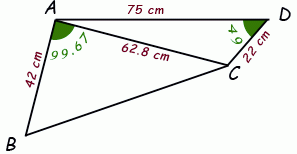Now we know two side lengths and the included angles for both triangles, so we can calculate the area of the quadrilateral.
Area of quad. ABCD = Area of tri. ABC + Area of tri. CDA
= ½(AB)(AC)Sin(CAB) + ½(AD)(CD)Sin(CDA)
= ½(42)(62.8)Sin(99.67°) + ½(75)(22)Sin(49°)
= 1922.7 cm2.
Solve your own problem the same way, Courtney.
Cheers,
Stephen La Rocque.
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.