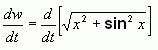Hi David.

The question involves the distance between the origin and a point on a graph, so I first think about how to calculate distances on a graph.

You can demonstrate to yourself that the distance from the origin to any point (x,y) on a cartesian graph is simply the square root of the sum of the squares x² and y². This is because the distance is the hypotenuse of a right triangle whose other sides are x and y, so Pythagoras gives us this expression.

So I start by calling the distance w and I write the equation:

Next, I need to know something about x and y. We are given the equation y = sin x, so I can substitute sin x in for y in my equation.

That's good: one equation with two variables. Now I look at the question again. It is asking for the "rate of change of the distance". Well, I know that that is the derivative of the distance with respect to time, which in variables means dw/dt. To find that, I have to take the derivative of both sides of my equation:

Clearly, I next would have to take the derivative of that expression and I'm going to need the chain rule more than once. I hope you have been studying the chain rule, David, because I'll leave the derivation to you. You will get, on the left side of the equal sign, an expression with x in it as well as dx/dt in it.

The last step is to look at a particular value of dx/dt. You simply substitute in what you are given (that dx/dt equals 2 cm/sec) and simplify. You will still have the value x in there, of course, because you weren't given a value for it. So don't expect a single number as your answer.

To review, when solving this kind of question, I

1. Look for a relevant equation that I can build on. In this case it was the distance formula (a variation of Pythagoras' Theorem),
2. Reduce the number of variables by using the substitution or elimination method of solving simultaneous equations when I look at other given equations and relationships in the question. In this case, that was applying the y = sin x relationship to it.
3. Examine closely what I need to isolate, if possible, on one side of the equal sign to get the quantity or expression actually asked for in the question. In this case, that was recognizing that I'm asked for dw/dt and solving for that. Then simplify what is on the other side of the equal sign (I left that for you to do).
4. Insert known values for the variables I have. In this case, I was given dx/dt = 2 cm/sec.
5. Simplify the answer.

Hope this helps,
Stephen La Rocque.