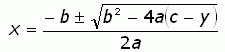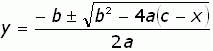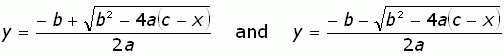Inverse of a quadratic function

HOME

Math Central

Quandaries & Queries

Question from Elliot, a teacher:

Hi: I'm a special education tchr trying to demonstrate how to find the inverse (using algebra) of quadratic functions. Any help would be greatly appreciated. Thanx.

Hi Elliot.

The inverse of a function f is a function g such that g(f(x)) = x.

So if you have the function f(x) = ax² + bx + c (a general quadratic function), then g(f(x)) must give you the original value x. You should already see the problem: there will be two functions, not one, since a function must provide a unique value in its range for each value in its domain and a quadratic maps two values to one (for example, 2² = (-2)² = 4).

But with that in mind, we can carry on.

y = ax² + bx + c

0 = ax² + bx + (c - y)

Using the quadratic formula, we get the following expression for x:

When we deal with the inverse, we have to swap the x and y terms:

But this maps two range values to a single domain value, so it isn't actually a function. The inverse of the quadratic is the curve formed by the union of the following two functions:

Cheers,
Stephen La Rocque and Harley Weston.

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.