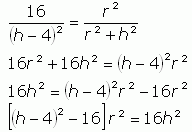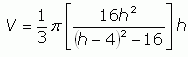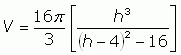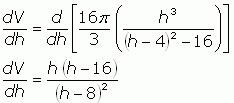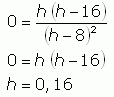Hi Eva.

For a fixed sized sphere to be inscribed in a variable cone, the cone could be short and wide or tall and narrow, with any variation in between:

The volume (V) of a cone is given by the formula

(1)

We need to know, however, how r is related to h and that comes from knowledge of the sphere being inscribed in the cone. Here is a two dimensional cross-sectional schematic that will help:

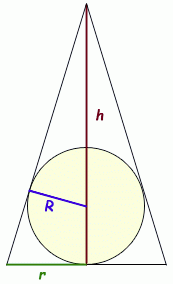
(Notice that I am using small r for the radius of the cone base and capital R for the radius of the sphere.)

I hope you can see that we have similar right triangles in this diagram. With similar triangles, the ratios of corresponding side lengths are equal. So in the small triangle, the ratio R/(h-R) is the short leg over the hypotenuse. In the larger right triangle, the short leg is r, but the hypotenuse is unknown. Yet through Pythagorus, we know that the square of the hypotenuse = r² + h². Thus, the following ratios are equal:

We know the radius R of the sphere is 4 cm, so let's substitute that in:

Now let's square both sides and solve this for r²:

(2)

So this shows how r relates to h. Now we can substitute this expression in (2) for r² into place in equation (1):

	(3)

Finally now we have an expression for the volume (V) of the cone in terms of its height (h) under the constraint that it inscribes a sphere of 4cm radius.

We are ready to find the minimum of this function, so we take the derivative with respect to h of both sides. You will need to use several derivative rules and show all your work, but I'll skip straight to the answer:

The minimum of this function occurs at a critical point, that is, when the derivative equals 0, so let's solve for that:

From the context of the problem, you can see that h must be more than twice R, in other words h > 8, so this means the only critical point is at h = 16cm. You could use the second derivative rule to satisfy yourself that this is a minimum rather than a maximum if you wish.

Now that you know h, you can plug it into equation (2) to find r² and then use those two values in equation (1) to get the minimum volume.

Cheers,
Stephen La Rocque.