Hi Gina.

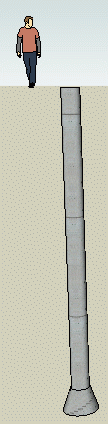I'm no concrete or construction expert, but I think the shape you are describing is what I've drawn here on the right side of the page.

You don't say how tall the belled-out portion is, so I am going to assume a 2 foot high bell.

As well, I will assume that your measurements are the circumferences of the pier. Most piers are in that range.

The shape therefore is that of a cylinder with a frustum for the base.

Let r = the radius of the pier.
Let R = the radius of the base of the bell.
Let h = the height of the pier (excluding the bell).
Let H = the height of the bell.

Then the volume of the shaft is πhr². The volume of the bell is the volume of the frustum that is H units high, with top radius r and bottom radius R.

The volume of a frustum is simply the difference between the volume of a cone minus the volume of the cone removed from the top to create the frustum.

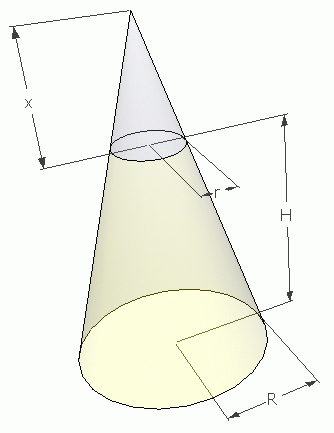Volume of a right circular frustum:

Using the diagram on the right, we can subtract the blue cone from the full cone to get the frustrum volume.

Notice that there are similar triangles in here, so the ratios of corresponding sides are equal. This means

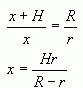
Now derive the formula for the frustrum's volume:

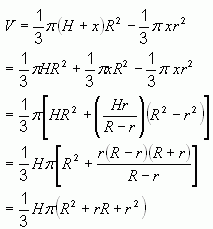
So the volume of the whole pier (shaft and bell) is the sum of these:

V = πhr² + (πH/3)(R² + rR + r²)

(Which is a formula you can use if my interpretation of your numbers or my assumptions are incorrect.)

Based on my assumptions though, here is the calculation:

First convert the measurements to the same units (I'll use inches for now):

h = 24 x 12 = 288",
r = 54 / (2π) = 8.59",
H = 2 x 12 = 24",
R = 108 / (2π) = 17.19"

Then use the formula we created to find the volume:

Volume
= πhr² + (πH/3)(R² + rR + r²)
= (3.1416)(288)(8.59)² + ( (3.1416)(24) / 3 ) ( (17.19)² + (8.59)(17.19) + (8.59)² )
= 79754 inches³.

Now to convert this to cubic yards, remember that 1 yard = 36 inches, so 1³ yard³ = 36³ inches³. Thus, we divide by 36³ to turn cubic inches into cubic yards: 79754 / 36³ = 1.71 cubic yards.

Cheers,
Stephen La Rocque.