| |||
| Math Central | Quandaries & Queries |
|
Question from Imaiya, a student: |
Hi Imaiya,
We're glad to help! It's always encouraging to hear that our site is useful for people and if you have ideas or suggestions for the site, let us know by emailing us at ![]() .
.
Now on to your question:
Each digit represents another power of the base. So think about base 10 numbers. Reading leftwards from the decimal, we have places that represent 100, 101, 102, 103, etc. You can see that 2007 is composed of 2 x 103 + 0 x 102 + 0 x 101 + 7 x 100.
Now let's think about base 8. If I have the base 8 number 3708 (we use a subscript after a number to show that it is to be interpreted in that base rather than the normal base 10) then I know that the places (again leftwards from the decimal) denote 80, 81, 82, etc. So 3708 = 3 x 82 + 7 x 81 + 0 x 80.
When we multiply numbers in other bases, we can do it two ways:
First method: Convert both numbers to base 10, multiply them normally, then convert that back to the desired base. This is usually preferable when multiplying numbers of different bases.
Here's an example: multiply 4556 by 7059 and express the product in base 4.
- Convert to base 10:
4556 = 4 x 62 + 5 x 61 + 5 x 60 = 144 + 30 + 5 = 179.
7059 = 7 x 92 + 0 x 91 + 5 x 90 = 567 + 5 = 572. - Multiply normally:
179 x 572 = 102388. - Convert to base 4:
102388 / 4 = 25597 remainder 0.
25597 / 4 = 6399 remander 1.
6399 / 4 = 1599 remainder 3.
1599 / 4 = 399 remainder 3.
399 / 4 = 99 remainder 3.
99 / 4 = 24 remainder 3.
24 / 4 = 6 remainder 0.
6 / 4 = 1 remainder 2.
1 / 4 = 0 remainder 1.
(reading the remainders backwards) this gives the final answer 1203333104.
Second method: Build a times table for the base you are using. This only works if the two factors are the same base.
For example, your first question was to solve 345 x 425:
| Base 5 times table |
0 | 1 | 2 | 3 | 4 |
| 0 | 0 | ||||
| 1 | 0 | 1 | |||
| 2 | 0 | 2 | 4 | ||
| 3 | 0 | 3 | 11 | 14 | |
| 4 | 0 | 4 | 13 | 22 | 31 |
Now multiply it as you would with base 10, but using this times table. Remember to use base 5 when carrying as well:
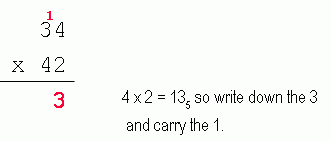

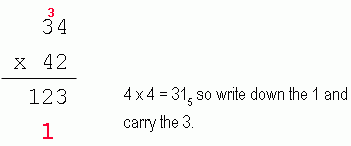


So the answer is 31335.
I hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.