Hi Jessica.

I'll demonstrate how to solve your problem by using Canadian coins and you can apply the method to your own question.

Penny: 19.05 mm diameter
Nickel: 21.2 mm
Dime: 18.03 mm
Quarter: 23.88 mm
Loonie: 26.5 mm
Toonie: 28 mm

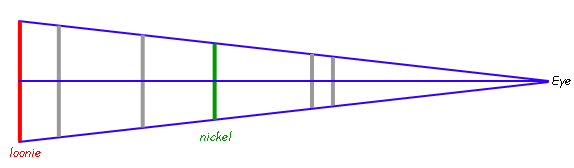
Part (a) is simply a matter of lining things up by size. The smallest coin would be nearest your eye.

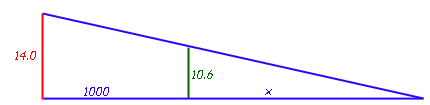
Now let's examine the geometry of the situation when someone looks along the central axis of these coins when they are lined up to be equal apparent size. I'm going to make the distance between the toonie and the nickel 1000 units:

Notice that if we draw that central axis, we can view this as similar right triangles. This means we can identify the side lengths using radii:

With similar triangles, the ratios of corresponding sides are the same, so:

10.6 / x = 14.0 / (1000 + x)

which reduces to

x = 3118 (rounded off).

And so the distance from your eye to the center of the toonie would be 4118.

Now you can use this value to determine the distances (from your eye) of the centers of the other coins:

Loonie:

4118 / 14.0= d / 13.25
d = 3897

Quarter:

4118 / 14.0= d / 11.94
d = 3512

Penny:

4118 / 14.0= d / 9.525
d = 2802

Dime:

4118 / 14.0= d / 9.015
d = 2652

Finally, the angle at the eye is twice the small angle of the right triangle. And using the arctangent function, we can find its size:

2 tan^-1(14.0/4118) = 0.39 degrees.

Try the same approach with your coins, Jessica.

Cheers,
Stephen La Rocque.