Juan, we have two responses for you:

Juan,

I drew a diagram of the largest sphere inside a cone.

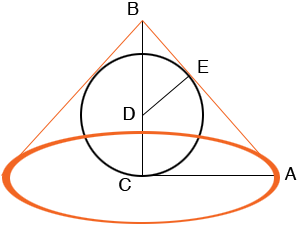
Since this is the largest possible sphere inside the cone the sphere touches the cone at E and thus AB is a tangent to the sphere at E and hence angle DEB is a right angle. Thus the triangles DEB and ABC have one angle in common, angle EBC, and each has a right angle, angles DEB and BCA. Thus angles BDE and CAD are congruent and hence triangles DEB and ABC are similar. Therefore

|BD|/|DE| = |AB|/|CA|.

|BD| is the height of the cone minus the radius of the sphere.
|DE| is the radius of the sphere.
|AB| you can find using Pythagoras' theorem.
|CA| is the radius of the cone.

This will allow you to solve for the radius of the sphere.

Penny

Hi JB.

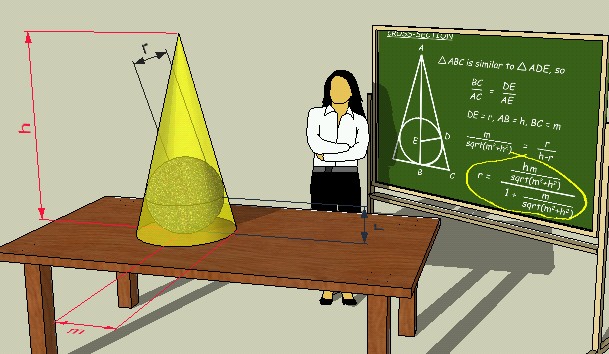
Take a look at the chalkboard and the dimensions of the cone and sphere inside.

Cones come in many sizes and shapes. I have a right circular cone of height h units and with radius m.

The corresponding largest sphere has radius r.

By examining the cross section, we can see similar right triangles. With similar triangles, the ratios of the sides are the same. We can use Pythagoras to compute the length of the hypotenuse of the larger triangle.

Then it is just a matter of solving for r. This gives a function in h and m that produces the radius of the largest sphere inscribed in it.

Here's a close-up of the chalkboard:

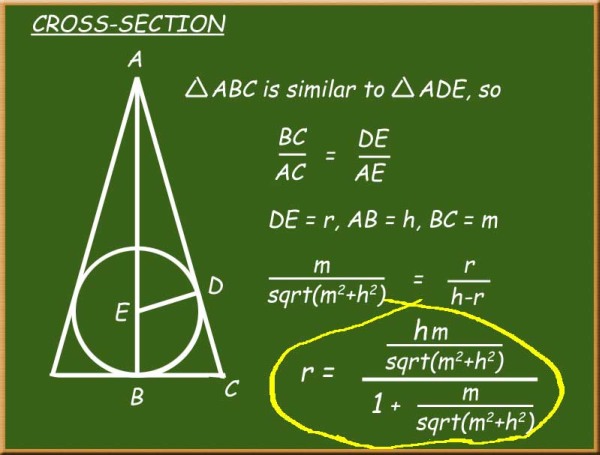
Cheers,
Stephen La Rocque.