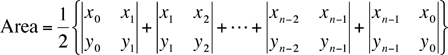Hi Lynda.

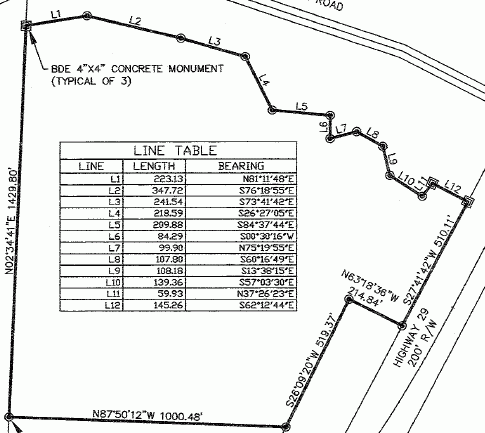
This is indeed a complicated bit of work! For a piece of land with this many sides (Seventeen!), all of them straight sides, I think using a specialized surveying method makes sense. I first learned about two such methods here on Math Central when our math consultant Chris Fisher described them in this message.

Chris describes the Surveyor's Area formula, which needs (x, y) Cartesian coordinates of each vertex, ordered in a counter-clockwise fashion begining at the origin. Then it uses 2 by 2 array determinants to find the area:

So we need to convert your lengths and directions into a counter-clockwise series of x,y coordinates. We should get the same answer wherever we start, so I'll choose the concrete monument and work counter-clockwise.

Unfortunately, the directions are given in a clockwise fashion, so I need to account for that in my computations.

We start by laying our cartesian graph's origin (0,0) at the monument with North along the positive y axis and head counter-clockwise, which takes us southish. That line is labelled as N02°34'41"E from the south point to the monument. Using standard polar angles, we know that the direction N02°34'41"E means the counterclockwise angle from the positive x-axis is 90° - 02°34'41 = 87°25'19". But since this measurement was in the wrong direction (we are going the opposite way), we turn it around by adding 180 degrees to it: 267°25'19". The length of the side times the sine of this angle is the distance northwards (+y) and the length of the side times the cosine of this angle is the distance eastwards (+x). Since we are going mostly south and a little west, both of these are negative.

The first side is 1429.80 feet long, at the proper polar angle 267°25'19". So the next point is:

(0 + 1429.80 cos(267°25'19"), 0 + 1429.80 sin(267°25'19") )
= ( -64.3129, -1428.3529 ).

The next side is 1000.48 feet long, with the reverse bearing of n87°50'12"W. That corresponds to a proper 357°09'48". So the next point is:

(-64.3129 + 1000.48 cos(357°09'48"), -1428.3529 + 1000.48 sin(357°09'48") )
= ( 935.4540, -1466.1193 ).

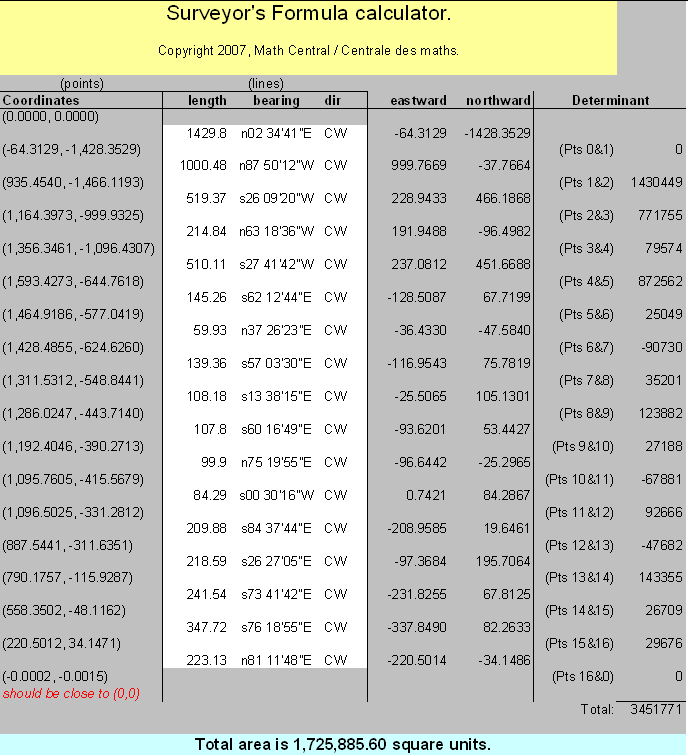
And so on, for all the corners. For each side, we want the determinant value. So for example, in this second side, the determinant is x₁y₂ - x₂y₁, which is -64.3129(-1466.1193)-935.4540(-1428.3529) = 1430449. When we add the determinants for all the sides and divide the sum by two, we have the area.

Clearly, putting these calculations in a spreadsheet will reduce the tedium:

(You can download the spreadsheet in MS excel format if you like).

Therefore, this shape is 1.725 million square feet. Since there are 43560 square feet in one acre, this is 1725885/43560 = 39.6 acres. Is that close to what the seller reports or the government registry says?

Cheers,
Stephen La Rocque.