Lots of them.
It depends on what you know about the cone.

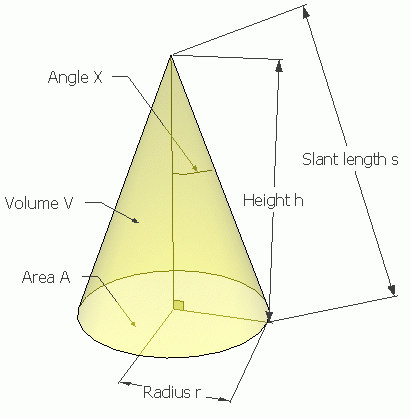
Here is a cone with a few things identified on it. I'm assuming you have what we call a right circular single-napped cone, which is a cone that has a circle for a base and the tip of it is centered over the circle.

The calculations mostly rely on the fact that their is a right angle at the bottom, so you can make a right triangle with the radius r, the height h and the slant s. The angle X is also in the triangle.

If you know any two things on this diagram, you can find any of the others.

For example, if you know the height h and the angle X, you can use the trig function TAN (tangent) to find the radius:

r = h tan(X).

And of course since the diameter is just twice the radius,

diameter = 2 h tan(X).

If you know want the area of a circle, it is calculated using A = π r², so we can put the two equations together and we get this:

A = π ( h tan(X) )².

The volume V of a cone is

V = (1/3) h A.

So if you knew the height h and the volume V and wanted the area, you would re-arrange this algebraically into:

A = 3V / h.

If you know the slant length s and the angle X, you can use the trig function SIN (sine) to find the radius r:

r = s sin(X).

And we can use this to find the area A again by combining it with A = π r² :

A = π ( s sin(X) )²

Let's say you wanted to know the volume and all you have is the slant s and the angle X. This takes a few steps:

First find the Area A in terms of s and X, which we just did: A = π ( s sin(X) )². Now we need h because V = (1/3) h A. But we can use the COS (cosine) function to find h if we know X and s:

h = s cos(X).

If we combine these three equations, we get:

V = (1/3) ( s cos(X) ) π ( s sin(X) )²

which will work, but we can reduce it using trig identities to:

V = [π s² sin (2X) ] / 6.

See what else you can figure out.

Cheers,
Stephen La Rocque.