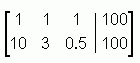Hi Marion,

You also know that you are buying 100 animals so x + y + z = 100.

But you are dealing with 3 unknowns so you'd need three equations to get a unique solution.  Without more information you cannot solve this system of equations to get a unique solution.  By more information I mean something like "the number of chickens purchased must be three times the number of cows" or some such other information.  But it allows you to get a third equation.

Without a third equation, the best you can do is to come up with a set of possibilities where there is a relationship between the numbers of animals.  To solve this type of system, set up and solve an augmented 2x3 matrix:

You may find that the relationships found in solving the matrix can be "limited" by the intention that the solutions represent whole number values only.

If matrices are not the intended method for solving, the only other method I could suggest is "guess and check".

Making a chart of all the possibilities would take a long time, but you'd eventually get the answers.

Not sure this helped much,
Leeanne

P.S.  HINT:  I did solve the matrix and I know that there are only 2 possible valid solutions.  Both involve the cows being a multiple of 5.