| |||
| Math Central | Quandaries & Queries |
|
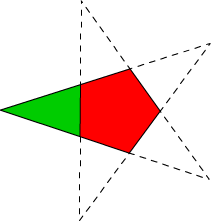
What is the area of the green part, in square centimetres? (Please round up to the nearest whole number) |
Hi Olivia.
The green triangle is isosceles, so if you know the measure of the angle between the common sides (the outside tip) and the length of the base (the side shared with the red pentagon), then you can find the area of the triangle.
First, the angle at the tip: Recall that the sum of the angles of a quadrilateral is 360 degrees. You should also know that the sum of the angles of a 5-sided figure is 540, because for any closed n-gon, the sum of the angles is 180(n-2).
For a regular pentagon, as in your diagram, all the angles are alike, so each interior angle is 540/5 = 108 degrees.
Now think of the quadrilateral that is coloured (ignore the colour and the common side shared by the triangle and pentagon. That is a four sided shape, so the total of its angles is 360. But you know from before that the measure of three of the angles is 108 each.
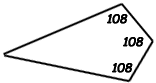
So the remaining angle (the tip of the triangle) is 360 - 3(108) = 360 - 324 = 36 degrees.
Now that we know the measure of the angle, we need the length of the base of the triangle, which is the same as the length of the side of a regular pentagon whose area is known.
Let's draw the center of the pentagon and divide it into 5 congruent triangles, then bisect one of those 5 into two congruent right triangles:
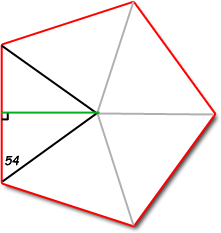
By symmetry, you should see that the 108 degree interior angles of the pentagon make the 54 degree angles. Also by symmetry, the five triangles are isosceles, so when we subdivide one of them (with the green line), we bisect the side length with a perpendicular. Thus we have divided the pentagon into the equivalent 10 right triangles with a 54 degree angle.
Let's label a few things on this right triangle:
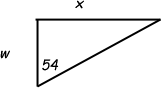
What is the area of this triangle? The area of any triangle is half the base times the height, so the area of this triangle is ½xw. Since there are ten of these triangles in the pentagon, the pentagon's area is 10(½xw). But you are told this is 800 cm2, so 800 = 10(½xw) which reduces to 160 = xw.
Using trigonometry, we know that the tangent of the 54 degree angle equals the opposite length over the adjacent length, so tan(54) = x/w, which we can rewrite as w tan(54) = x.
Since this equals x, let's substitute it into our earlier equation:
160 = xw = (w tan(54)) w = w2 tan(54).
Now we can find w:
160 / tan(54) = w2.
w = 10.782 cm.
Now let's divide that green isosceles triangle the same way:
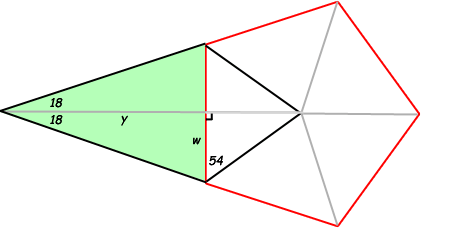
We've bisected the tip angle, so 36/2 = 18 degrees. The green triangle therefore is the sum of the two congruent right triangles. Since each of these has an area of ½wy, the area in green is just wy.
Again using trigonometry, tan(18) = w/y, so y = w/tan(18). This means the green area is wy = w2/tan(18).
And since w = 10.782 cm, we have
Green area = (10.782)2 / tan(18) = 357.8 cm2.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.