Hi Paula.

2x-3y=9 is not a point, it is a line which represents a function.

I think when the question says "find the function for y" it means to convert the equation into the form y = mx + b. Here, m and b are numbers. So it means the same thing as "solve for y". You don't have to have the equation represented as a function of y in order to plot it, but it sure makes things easy. So your assumption is probably correct and your son is meant to use the y = mx + b form to plot the line.

So the first step is to convert the equation to that form:

2x - 3y = 9

-2x + 2x - 3y = -2x + 9                                     subtracting 2x from both sides

-3y = -2x + 9                                                    simplify

(-3y) / (-3) = (-2x + 9) / (-3)                              dividing both sides by -3

y = (2/3)x - 3.                                                 simplified.

So the equivalent form in y = mx + b form is y = (2/3)x - 3. m is the slope, and b is the y intercept.

So to plot the line on a graph, you start at the y intercept. The y intercept is the point where the line crosses the y (vertical) axis. So that point is (0, b) which in our case is (0, -3).

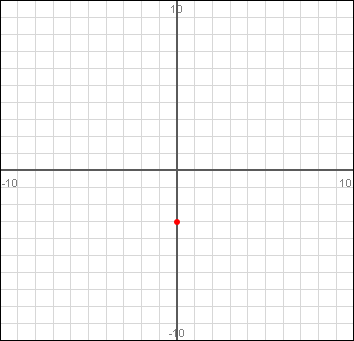
Next, you use the slope m = 2/3 to find out where to plot another point. The slope is the "rise" over the
"run" which means upwards over rightwards. So for 2/3, you go up 2 units and to the right 3 units and put down another point for the line:

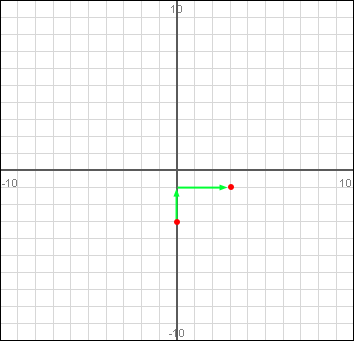
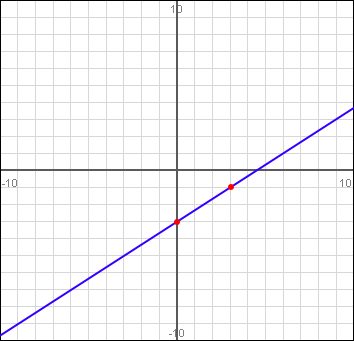
Now that you have two points, you can use a ruler to just draw the line through the two points to finish the graph:

Cheers,
Stephen La Rocque.