Hi Peter.

I drew a diagram and labelled those and other angles with variables from the Greek alphabet, using rules of reflection to indicate which angles have the same measure as other angles:

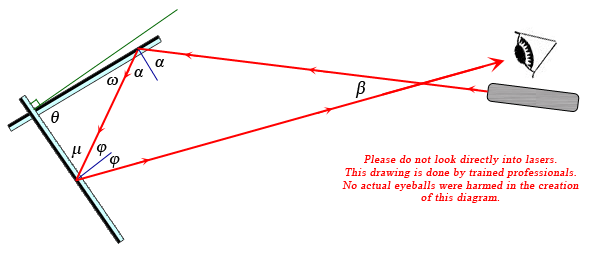
Note that the "angle of incidence" equals the "angle of reflection" as measured from the perpendicular to the mirror surfaces.

The sum of the angles of the red triangle is 180 degrees:

2α + 2φ + β = 180.

Also, we see that ω and α are complementary angles, so α = 90 - ω. For the same reason, φ= 90 - μ.

When we substitute this into the first equation, we get:

2(90 - ω) + 2(90 - μ) + β = 180.

We also know that the other triangle's angles add to 180 degrees: θ + μ + ω = 180. So ω = 180 - μ - θ.

Substituting this into the previous equation gives:

2(90 - (180 - μ - θ)) + 2(90 - μ) + β = 180.

Solve for β.

Cheers,
Stephen La Rocque.