Hi Priyanka.

I chose to draw points A, B and C vertically. The body is the yellow tick on the line (which the arrow points to). The black ball gives a visualization of the kind of thing that is happening. The position of the body on the black vertical line is the height of the black ball.

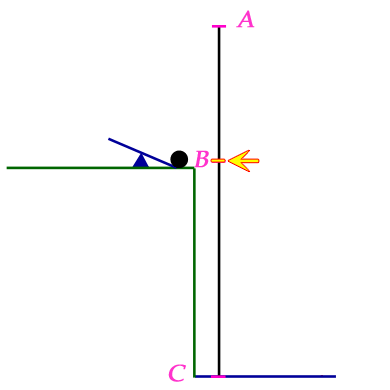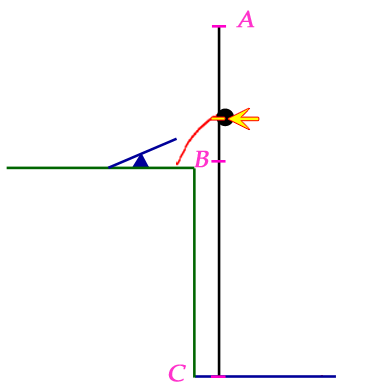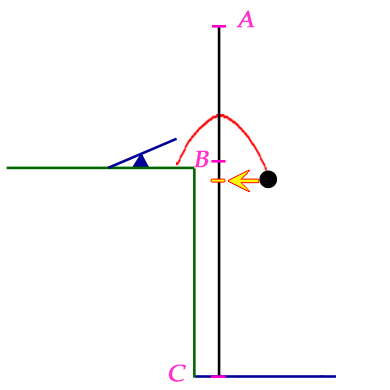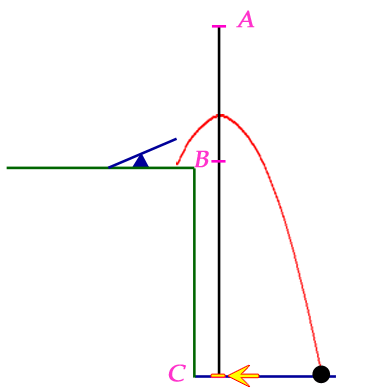The body begins by moving 3 m/s towards A (upwards). During its motion, it is experiencing an acceleration of 1 m/s² towards C (downwards).

The generalized equations of constantly accelerated motion are:

    d = v₀t + ½at² and

    v = v₀ + at.

Thus, if we consider "up" as positive, then v₀ = 3 m/s  and a = -1 m/s².

Together these equations can answer your question. The variable d is the displacement of the body above the initial position. So when d = -20 meters, you can solve for t using the first equation and get the answer to the first part of your question.

To answer the second part of your question, you need to first find how high above the initial position the body moves before starting its descent. To find this, you need to recognize that at the point where it starts moving down, the velocity is zero. Thus, you can use the second equation to find the time it takes to go from start to the top. Then you can use that time t in the first equation to find the displacement above the initial position. That lets you calculate the total distance travelled.

Cheers,
Stephen La Rocque.