Hi Rajesh.

The three most important facts to use in solving this question are

1. Each triangle has angles totalling 180 degrees and
2. Each right angle (the corners of the square) is 90 degrees
3. The angles opposite common sides in an isosceles triangle are congruent.

First, you know the angles of an equilateral triangle are equal, so each is 180/3 = 60 degrees. And since the bottom corners of the square are 90 degrees each, the remaining angles are 30 degrees each. Let's use symmetry and use variables to represent the other angles. We get this diagram:

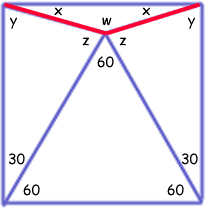
Recall that since this is a square sharing a side with an equilateral triangle, so all the blue sides are the same length. Therefore the other three triangles are isosceles. Thus using the three foundation principles I mentioned:

   x + y = 90
   2x + w = 180
   y + z + 30 = 180
   y = z

This gives us four equations with four unknowns.

You can use the elimination and/or substitution methods for simultaneous equations to solve the rest.

Here's an example of solving four equations in four unknowns.

Cheers,
Stephen La Rocque and Penny Nom.