Hi Rajesh.

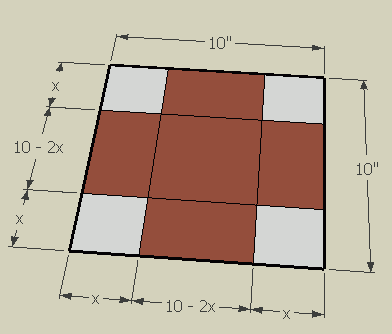
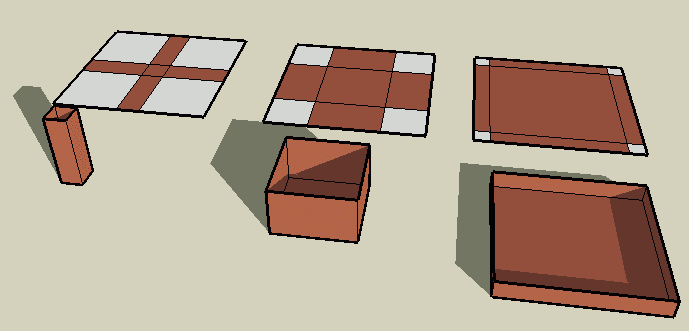
I am sure you have recognized that a very thin flat box will not hold much volume, and neither will a very tall box with a small base. There must be some value between the extremes that maximizes the volume of the box.

Let's consider this algebraically:

So the volume of the box is its length times width times depth:

Now take the derivative of both sides of this equation with respect to the variable x:

You will need to use the chain rule to solve this. Remember that a really narrow box has a small volume, as does a really thin box, but in between these extremes, we find a maximum volume. This is a critical point, so the derivative at the this point is zero. Thus, all you need to do is solve for x by making dV/dx = 0:

Solve for x.

Cheers,
Stephen La Rocque.