Hi Robert.

I assume this isn't a "trick question" in that you wouldn't have to drive fast at all; just wait for 24 hours.

The wording is a little awkward, because to see the sun "rise" it must be moving upwards compared to the horizon. Since it has already crested the horizon, we'd have to sprint so fast that it moves backwards and slow down so it can re-crest the horizon. I don't think that is what you are intending to ask. So I'll answer the question "How fast must I drive to keep the sunrise in place on the horizon?"

Since the earth revolves in 24 hours regardless of lattitude, I clearly need to travel at the speed equal to the circumference of the earth (at my current lattitude) per 24 hours.

So I need to find out the circumference of the earth at my current lattitude.

I live in Regina, Saskatchewan, Canada, so I'm going to show you how I calculate the earth's circumference at this lattitude and you can do the same for where you live (or perhaps the Bonneville salt flats in Utah).

My lattitude is 50°30'. Since there are 60 minutes in one degree of lattitude, this is 50.5°.

This means that the angle formed in the center of the earth by two particular radii is 50.5. The two radii are of course the radius to my location and the radius to the equator of the earth at my longitude. I can draw the following diagram:

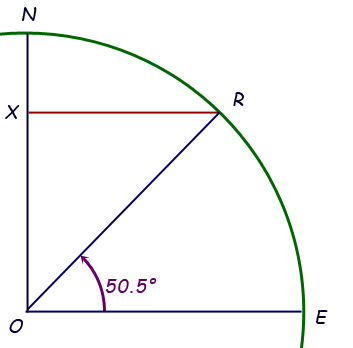
This is a partial cross-section of the earth. R is the location of Regina, E is the equator, N is the north pole, O is the center of the earth and the line segment XR is the radius corresponding to the circumference of the earth at my lattitude. If I know XR, then the speed I need to travel is (2π XR) / 24 in distance per hour.

When we have a line that crosses a pair of lines that are parallel, then the alternate interior angles are equal. That means mEOR = mORX. Since XR is perpendicular to the earth's axis ON, this is a right triangle.

So XR/OR = cosine 50.5°, in other words,

     XR = OR cos(50.5°).

The radius of the earth is known to be 6378 km, so

     XR = (6378 km) cos(50.5°) = 4057 km.

And now I can calculate the circumference at my lattitude:

2π (XR) = 2π (4057 km) = 25490 km.

I would need to travel that far in 24 hours, so that works out to

25490 km / 24 hr = 1062 km/hr. Certainly possible to do in a modern jetliner.

Now you try it with a location of your choosing. You'll need to find the lattitude for that location, and if you want things in miles per hour, you'll need to find the radius of the earth in miles. If you choose somewhere closer to the equator that Regina, you'll need to go faster than me. If you are closer to one of the poles, you would go slower.

Cheers,
Stephen La Rocque.