Hi Saurabh.

An isosceles triangle with an angle of 120 degrees has 30 degrees for each of the other two angles.

Let's draw the triangle and the inscribed circle. I'll also draw extra lines and label points to assist in the analysis of the diagram:

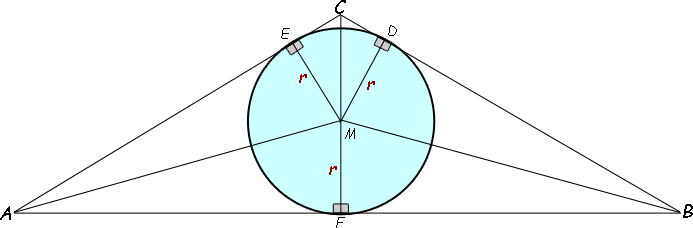
As you can see, BCA is the 120 degree angle and r is given to you as √3.

You should see very many congruent isosceles triangles in this diagram. In fact, the triangle ABC is composed of four copies of triangle AFM and two copies of triangle MCE. So simply by finding the area of those two right triangles, you can find the area of the large triangle ABC.

Calculate the angles involved. Everything is being bisected, so that should be easy for you.

Then use sine, cosine or tangent (as you deem appropriate) to determine the lengths AF and CE. That lets you find the areas of triangles AFM and MCE.

Finally, calculate the area of ABC by adding the areas of the component triangles.

Cheers,
Stephen La Rocque.