| |||
| Math Central | Quandaries & Queries |
|
Question from Vivek, a student: what are the properties of a regular hexagon inscribed in a circle. If the radius of the circle is given then how to find the side of the regular hexagon |
Hi Vivek.
If you draw a hexagon inscribed in a circle and draw radii to the corners of the hexagon, you will create isosceles triangles, six of them.
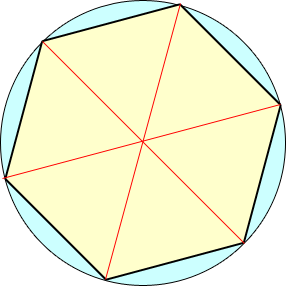
With any isosceles triangle, the bisector of the shared vertex is a perpendicular bisector of the opposite side. So I can draw these as well, making twelve congruent right triangles:
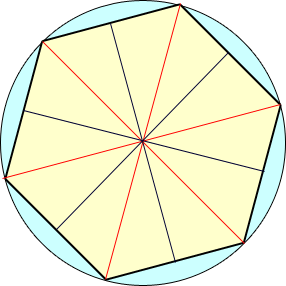
The side length of the hexagon is two of the short sides of the right triangle. The short side of the right triangle is opposite the angle at the circle's center. So if we know the measure of the angle at the center, we can use the sine function to find the side length of the hexagon, since the radius is the hypotenuse:
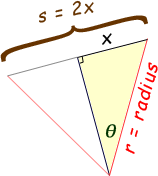
Thus, s = 2x = 2 (r sin θ). Now you just need to determine what θ equals, based on your knowledge of circles.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.