| |||
| Math Central | Quandaries & Queries |
|
I am trying to figure out how big a piece of wood I need for a variant of chess I thought up. The board essentially is a set of 6 concentric rings with an empty space in the center, each ring consisting of 24 spaces - so essentially 6 concentric 24-sided polygonal rings made up of trapezoidal spaces. I know the interior angle of the shape (15 degrees), but I can't figure out the size this thing should be. All I know is that the innermost ring will have the smallest spaces, and that those spaces need to be able to accommodate chess pieces 3/4" wide without them overlapping onto neighboring spaces. That is to say, the short parallel side of the trapezoidal space on the innermost ring should be at least 3/4". But I have no clue how to extrapolate the full diameter of the board from that one measurement. HELP! Adam Goss |
Hi Adam.
You are right: 15 degrees separates the cells from one another. So the innermost "edge" will be 0.75 inches on each side. That forms an isosceles triangle with the center, and the central angle is 15 degrees. That means the distance from the center to a vertex is one of the common sides. If you bisect this isosceles triangle, you get a right triangle whose hypotenuse is this center-to-vertex length, one leg is 0.375 inches and the angle opposite that leg is 7.5 degrees.
To calculate the length of the hypotenuse, you can use the Sine relationship. Sin(7.5) = 0.375/h. This means h = 2.873, or roughly 2 7/8". So that means the central "dead" space (perhaps you can use it for the rules) would be twice this length between opposite vertices of the the 24-gon.
To make things simple, let's say each ring is 1 inch wide. That means the overall diameter is 2[6(1) + 2.875] = 17.75 inches from corner to corner.
Here's a sample (a higher-resolution version is here ).
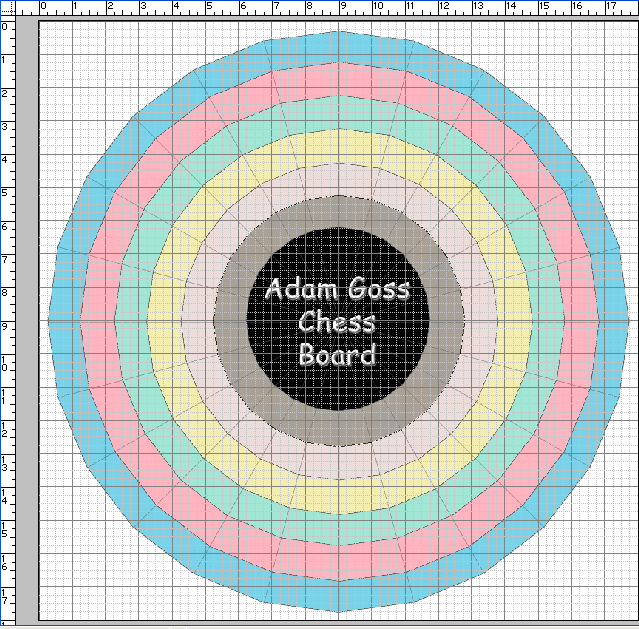
If you build it, send us a photograph please!
Cheers,
Stephen La Rocque
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.