| |||
| Math Central | Quandaries & Queries |
|
Radius of big circle 30cm, radius of small circle 10 cm. From the diagram, the radius from the tangent do not form a semicircle but at an angle. Find the perimeter of the band around both the circle. May need to use trigonometry to find reflex angle AOB, CMD and get the major arc length AB and minor arc length CD Alan. |
Alan,
I think we didn't get part of your attachment as we didn't see your solution, just the problem statement above and a diagram. I redrew the diagram you sent to have circles where the radii look like they are in the ratio of 1 to 3.
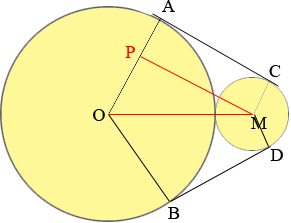
I drew the line MP to be parallel to CA and I joined the centres of the circles. The line OM passes through the point of tangency of the circles (Do you see why?) so |OM| = 3 + 1 = 4 cm. Also |PO| = 3 - 1 = 2. Since MP is parallel to AC angle MPO is a right angle. Can you now see the length of MP? If not Pythagoras can help. This gives you |AC| = |BD| = |PM|.
You can find the arc lengths you need if you can find the measures of the angles POM and OMP. Does you knowledge of the side lengths of the triangle POM tell you this? What is the cosine of the angle POM?
I hope this helps,
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.