Hi Annie,

I would draw a tree diagram. Here is mine for 2 draws. My assumption is that the choosing of bulbs from the box is without replacement.

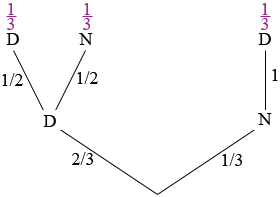
There are 3 bulbs in the box and two are defective so on the first draw you have a 2/3 probability of selecting a defective bulb and a 1/3 probability of drawing a bulb that is not defective.

If you draw a defective bulb then there are 2 bulbs remaining, one defective and one not defective. Thus on the second draw the probability of selecting a defective bulb is 1/2 and the probability of drawing a non-defective bulb is 1/2.

If your first draw was a non-defective bulb then the 2 remaining bulbs are both defective and hence the probability of drawing a defective bulb on the second draw is 1.

If you draw two bulbs then you take one of the three paths through the tree. Since 2/3 × 1/2 = 1/3 and 1/3 × 1 = 1/3, each of the three paths has a probability of 1/3.

What is the probability of choosing a non-defective bulb and a defective bulb in 2 draws?

If you chose a non-defective and a defective bulb you did so by either choosing a non-defective and then a defective or a defective and then a non-defective. Each possibility has probability 1/3 so the probability of choosing a non-defective and a defective bulb is 1/3 + 1/3 = 2/3.

What is the probability of choosing 3 defective bulbs followed by a non defective bulb?

Check to see if this question is correctly worded. If it is then the probability is 0 since you can't draw 3 defective bulbs, there are only 2.

What is the probability of choosing first 2 non defective bulbs followed by a defective bulb?

Extend the tree diagram another level to answer this question.

Penny