| |||
| Math Central | Quandaries & Queries |
|
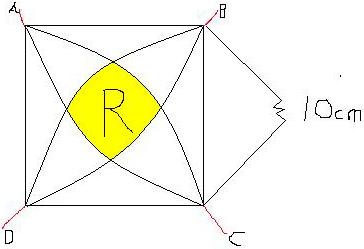
Question from Anthony, a student: I have a square where one side measures 10cm and within that square There are four equal quarter circles. Each quarter circles starts in a different corner of the square and I am trying to find area inside the overlap on the quarter circles. |
Hi Anthony,
We are not sure what your are doing. The circles might not overlap each other. These are 4 circles of radius of 5 cm.
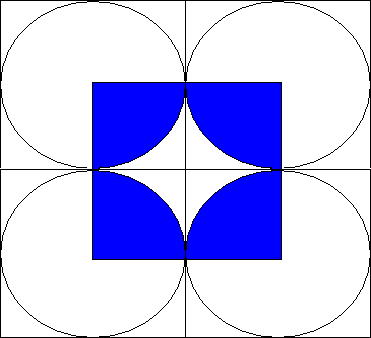
What happens if we increase the radius of the circle to 6cm?
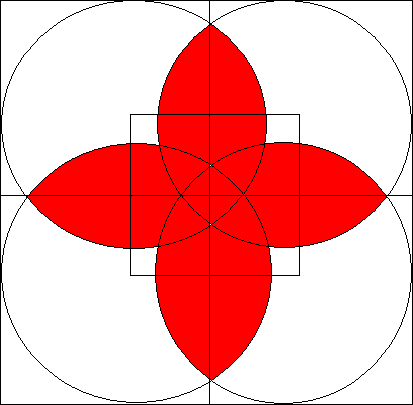
The area of the 4 quarter-circles inside the square is about 113 cm2 and the area of the square is 100 cm2 so about 13cm2 wouldn't fit in the square. This is the same as your area of overlap. How much the quarter circles overlap depends on the radius of the circles.
If you want to try it out for yourself try cutting a 10cm by 10cm square out of paper and circles of various sizes. If you quarter the circles and rearrange them you will see this is true.
Hope this helps,
Janice and Penny
Anthony wrote back
The answer what was given did not quite match the problem I had sent in.
I have attached a picture of the problem as close as I could to draw it to help you better under stand the problem.
I am trying to find the area of (R) What I need is the formula for doing so
Anthony,
I want to find 1/4 the area of the region enclosed by the 4 circles or radius 10, the region you labeled R.
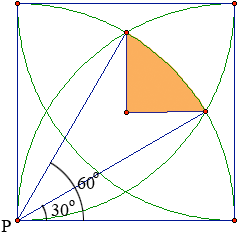
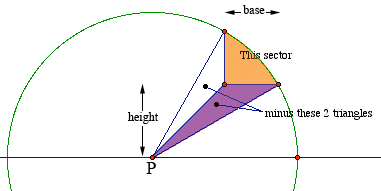
The way to determine that area is to note that it is 1/12 the area of the circle (from 30o to 60o)
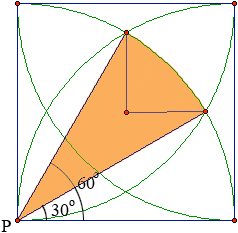
minus the area of two triangles whose base is 5(sqrt(3)) - 5 and height is 5.
Chris
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.