| |||
| Math Central | Quandaries & Queries |
|
Question from anthony, a student: A perfect circle with radius 100m is supported by four legs, 50m long. The circle is flat when all four legs are 50m long, and tilted when the legs are different in length. The four legs are spread evenly 90 degrees apart at 0, 90, 180, and 270. Find the high and low points in degree and height when the legs are 55m at 0 degree, 70m at 90 degree, 45m at 180 degree, and 30m at 270 degree. Not sure if they can be calculated using only 2 or 3 legs. I have tried by picking the two adjacent highest legs (55m and 70m) so I know the high point falls into the first quadrant. Then I tried using ratio to determine where the high point is, which I think high point should be closer to the 70m leg, I am not sure. If I can find the high point, the low point should be opposite to it. |
Anthony,
Are you sure the table has a radius of 100m? That's almost large enough to bee the roof of a football stadium.
First, one should subtract 50 from the legs to put the centre C of the table at the origin.
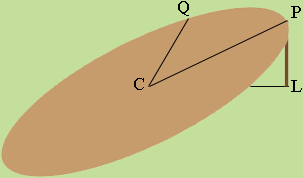
The point P, which is at the top of the leg which stands on the positive X-axis, is a distance |PL| = 5 am above the XY-plane. |CP| = 100 am and hence, by Pythagoras theorem, |CL| = 5√399 am Hence P has coordinates (5√399, 0, 5). Similarly the point Q, directly above the Y-axis has coordinates (0, 20√24, 20). The points C, P and Q can then be used to write the equation of the plane which contains the surface of the table. We got the equation to be
√(24 × 399) z = √24 x + √399 y.
The slope of the table top is steepest in the direction of the gradient and the gradient of this function is in the direction √24 i + √399 j.
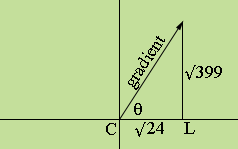
XY-Plane
Hence the measure of the angle θ is tan-1(√399/√24) = 76.2 degrees.
Chris and Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.