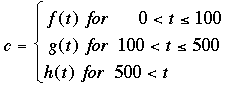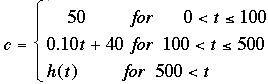An equation for a line with a changing slope

HOME

Math Central

Quandaries & Queries

Question from Ben, a student:

Is there anyway to write an equation for a line with a changing slope.
e.g. A cell phone company has a initial fee of 50$ paying for the first 100 minutes,
the rate then increases to 10 cents per minute, then at 500 minutes the rate is 5 cents
per minute.

If so please tell how.
Thanks

Ben,

I see this graphically so I began with a rough sketch of minutes against dollars. The graph is a flat line until the time reaches 100 minutes and then it increases at a slope of 0.10 dollars/minute. At 500 minutes the slope of the line decreases to 0.05 dollars/minute.

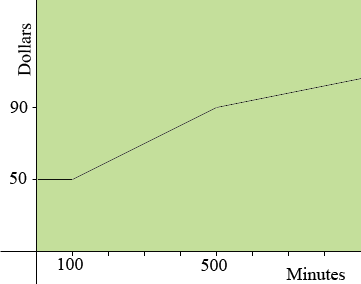
piecewise graph

This is sometimes called a piecewise function. The graph is in three pieces so I would write the function in 3 pieces.

where c is the cost in dollars and t is the time in minutes.

f(t) is the constant function f(t) = 50.

g(t) is the line with slope 0.10 and passing through (100, 50). I got g(t) = 0.10t + 40.

You can find h(t) and then the function is

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.