Bevaz,

Go to the Quandaries and Queries page on Math Central and use the Quick Search to search for the term working together to see how we have approached these problems. Yours is slightly more involved because of the three people but the idea is still the same.

I can get you started. Suppose A can complete the job in a days, B in b days and C in c days, then the rates at which they work are 1/a, 1/b and 1/c jobs/day. Hence A and B working together work at a rate of 1/a + 1/b jobs/day. Thus the amount of time they take for a job is

days.

But we know this is 6 days so

days.

Now look at the other two pairings. If you need more assistance write back.

Penny

Bevaz wrote back

so, a + b = 6 days
b + c = 20
c + a = 7.5 how to solve this? please help...

Bevaz,

For the equation 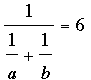I would first multiply both sides by 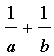to get

.

Writing the left side with the common denominator ab this equation becomes

6a + 6b = ab.

Now look at the other pairs, A with C and B with C.

Penny