Hi Billy. I don't know the formula, so I'm going to determine what it should be geometrically.

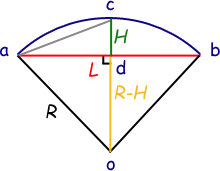
So I've drawn the arc "acb", where ab is the length across (L), cd is the height of the arc (H) and R is the radius. I've also drawn in a connecting line between a and c and from the center of the circle to the point d. Since oc is another radius of the circle, it equals R as well. That means since cd = H, then od = R - H.

First, it is very important to notice that the triangle ado is a right triangle. the lines ad and od are perpendicular. As well, from symmetry you should recognize that ad is half of ab, that is, ad = L/2.

So you have a right triangle ado, whose two legs are of length L/2 and R-H and the hypotenuse is length R.

Now let's use pythagoras. The square of the hypotenuse equals the sum of the squares of the legs:

R² = (L/2)² + (R-H)²

Let's simplify this and solve for R, the radius we want to know:
R² = L²/4 + R² - 2RH +H²
0 = L²/4 - 2RH +H²
2RH = L²/4 +H²
R = (L²/4 +H²) / (2H)
R = L²/8H + H/2

You had the formula (4H² + L²) / (8H). That is in fact equal to my equation! So we agree on the formula now.

Let's look at the values you gave me: length is 18.875 in and height is 37.75 in. Whoa! The height is way bigger than the length! So we actually have a big bubble. My diagram assumed that the height was smaller than the chord length. In fact, this means that the height is larger than the radius.

When I redraw the diagram with a large height compared to the chord length I get this:

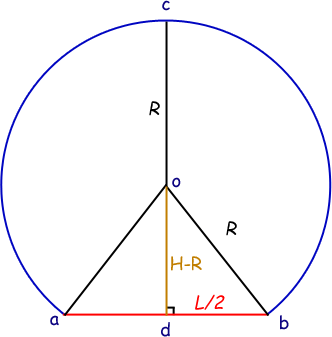
I notice that the only real difference it makes to my geometry is that instead of R-H in yellow, I have H-R (because the gold line is the whole height minus the top black part which is the radius R).

Do you recognize that - (H-R) = -H + R = R - H? So we have just got the negative of the value from earlier. But in Pythagoras' Theorem, we are squaring it. When we square a negative, we get a positive. So in fact, (R-H)² = (H-R)². This means we don't need to change our equation at all!

So let's plug in the numbers into your equation:
(4H² + L²)/8H
= ( 4 [37.75]² + [18.875]² ) / ( 8 [37.75] )
= ( 4 [1425.0625] + [356.265625] ) / 302
= 6056.515626 / 302
= 20.055 inches.

Then is the right answer: 20.055 inches (rounded off).

Hope this helps,
Stephen La Rocque.