Hi Carole,

I am going to do a similar problem.

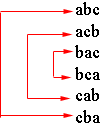
1. Find all possible arrangements of the three letters a, b and c.

If I start to write down an arrangement I need to choose a first letter. There are 3 choices. Once I write down the first letter I need to decide on a second letter. Since one has already been chosen there are 2 choices for the second letter. Thus there are 3 × 2 = 6 ways to write the first two letters. Once I have written down the first two letters there is only one possibility for the third letter and hence there are 6 possible arrangements of the letters a, b and c.

Here they are in a list

abc
acb
bac
bca
cab
cba

But you have two digits the same so let me make two of the letters the same.

2. Find all possible arrangements of the three letters a, b and a.

Notice that in the list generated in the first problem the arrangements go together in pairs. Every arrangement has a twin where the placement of the a and c are reversed.

If you write a in place of each c the list becomes

aba
aab
baa
baa
aab
aba

which collapses to

aba
aab
baa

Since the list collapsed in pairs the answer to question 2 is 3, half the answer to question 1.

Now try your problem,
Penny