| |||
| Math Central | Quandaries & Queries |
|
Question from Charlene, a student: A fixed circle lies in the plane. A triangle is drawn inside the circle with all three vertices on the circle and two of the vertices at the ends of a diameter. Where should the third vertex lie to maximize the perimeter of the triangle? |
Hi Charlene,
I let the diameter of the circle be d and the lengths of the other two sides of the triangle be x and y. The perimeter is then given by P = d + x + y.
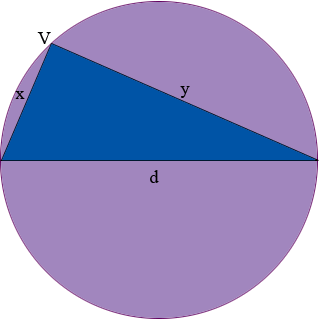
What does your intuition tell you should be the position of the vertex V to maximize the perimeter? Can you convince yourself, without calculus, that this is the correct answer?
The diameter d of the circle is a constant so P = d + x + y is a function of two variables x and y. To solve this problem using calculus you need to express P as a function of one variable. The key here is that the triangle is a right triangle since the angle subtended at the circumference of a circle by a diameter is a right angle. Pythagoras' theorem then gives you a relationship between x and y that allows you to express P as a function of one variable. Differentiate this expression and use you knowledge of calculus to maximize P. What is the position of V when the perimeter is maximized? was your intuition correct?
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.