Chew,

There are several issues here!

-Real world: I don't have to tell a teacher that these numbers may not represent teaching ability (and suggest absurd grade inflation)

-As a simple percentage problem: teacher B obviously has a higher proportion of A students within the sample observed. (I assume you knew that!)

-As a statistical inference problem, it's rather subtle. If you had to say the most likely (in the technical sense of "compatible with the data)" long-term success rate for each teacher, then it would be 90% for teacher A, 100% for teacher B. Just like the answers to the last question...

On the other hand, these are not the only long-term success rates that are reasonably compatible with the data. Say that over the long term only 50% of Teacher B's students get "A"'s; there would still be one chance in 32 of seeing results at least as good [and 1 chance in 16 of results at least as different] as given. The probability of Teacher A's 50 students obtaining 45 A's under the same assumptions is effectively zero. Thus, the data we have seen provide very strong evidence that the majority of Teacher A's students get A's, and only moderately strong evidence that the majority of teacher B's students do so.

This idea can be formalized in various ways. Several of them (eg, confidence intervals and hypothesis tests) will be inconclusive; they will say (rightly) that we cannot tell from the data which teacher is more successful.

The question we would like to answer is: for which teacher is the probability that _your_ child gets an A highest? We cannot answer this question meaningfully with classical statistical inference, which does not allow a probability to be assigned to a parameter like success rate. (It would be incorrect to make a "best guess" at each teacher's success rate and then treat these as if they were known parameters.)

Bayesian statistics allows us to do so but only if we have a so-called "prior distribution" for success rate. This represents the probability that a randomly selected teacher has a certain success rate.
We don't know what this is! However, the more data we have, the less the prior matters, and in one case at least we know quite a lot. We will use a "flat prior" assuming that a randomly selected teacher may have any success rate from 0 to 1 with equal probability.

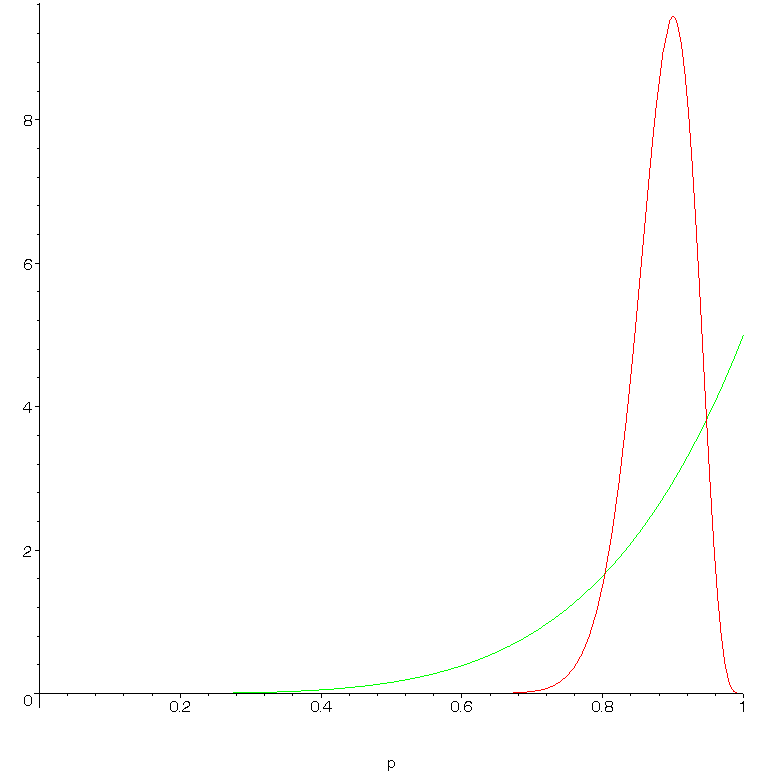
For teacher A the "posterior distribution" [representing a probability based on the prior _and_ the data] is roughly bell-shaped and peaks at 0.9 (see attached graph). Its average (this needs calculus or numerical integration) is about 0.88. For teacher B the curve peaks at 1 but spreads further to the left, representing a higher probability of low long-term results. And its average is 5/6 or about 0.83. Teacher A is thus - on the basis of information available - the safer bet.

Now, if the prior was different (say we knew that most teachers had success rates of 90% or higher) we might have reached a different conclusion; in the case of B at least we have very little data and our choice of prior will affect the outcome significantly. This is (one of the reasons) why some statisticians are dubious about Bayesian methods. However, this sensitivity to the prior is not hidden, and an experienced user can take the result at face value. It is certainly better than the naive approach of finding point estimates of 0.9 for A, 1 for B and reaching the opposite conclusion, which is certainly not supported by the data!

Good hunting!
RD

Chew,

I also have some problems with this question. As a parent I would like to see the data for these teachers for more than 1 class. If this is all that is available then my major question is "Does teacher B always have such small classes?" If so, then with no other information I would chosse teacher B.

Harley