Hi Connor,

Since the cross section is a semicircle and it is 10 a deep at the centre, the radius of the circle is 10 m. Thus every point on the surface of the canal is 10 m from the centre. To write an equation I am going to place the centre of the circle at the origin in the Cartesian plane. Thus the centre has coordinates (0, 0).

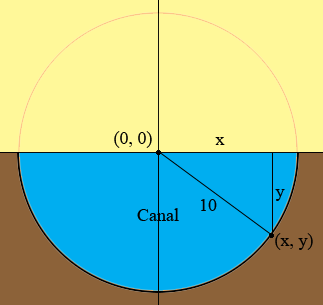
In my diagram I placed a point (x, y) on the surface of the canal and drew lines to construct a right triangle with sides of length x and y metres and hypotenuse 10 metres. What does Pythagoras theorem say about this triangle? This gives you a relationship between x and y but the requirement that (x, y) be on the lowe semicircle gives the further restriction that y ≤ 0.

Can you complete the problem now?

If you need more help write back,
Penny