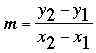Hi Conor,

I am going to show you two ways to write the equation of a line through two points, but I am going to use the points (2, -2) and (-4, 1).

For each of the two methods I am going to illustrate I need the slope m of the line so I'm going to find it first. The expression I have seen in most books is that the slope m of the line containing the two points (x₁, y₁) and (x₂, y₂) is

I think of it as "the difference between the y-coordinates divided by the difference between the x-coordinates". In my case I get (make sure you subtract the numerator and denominator in the same order)

Expression 1:

The first expression for a line I want to consider is

y - y₁ = m(x - x₁)

 

where (x₁, y₁) is some point on the line. I am going to use (x₁, y₁) = (-4, 1). It doesn't matter which of the two points I use. So I get

y - 1 = -1/2(x - (-4))
y - 1 = -1/2 (x + 4)

I would next multiply both sides by 2 to get

2y - 2 = -(x + 4)
2y - 2 = -x - 4

so

2y = -x - 2

If you want you can divide both sides by 2 to get

y = -1/2 x - 1

Expression 2:

The second expression for a line is

y = m x + b

where again m is the slope and b is some number. You already know m so the equation is

y = -1/2 x + b

and it only remains to find b. This you can do by substituting either point into the equation above. This time I am going to use the first point (2, -2). Substituting into the equation I get

-2 = -1/2 (2) + b
-2 = -1 + b

so

b = -2 + 1 = -1

Thus the equation is

y = -1/2 x - 1

Now try your two points.

Penny