Corey,

There are various possibilities. If you have a plywood with a nice, very straight, grain parallel to one side, and you don't plan to cover it, you could consider cutting seven triangles and two half-triangles as shown

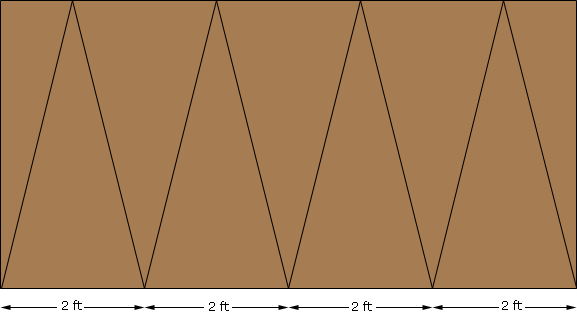
and assembling them points-in over an appropriate frame; the grain will give a lovely octagonal pattern.

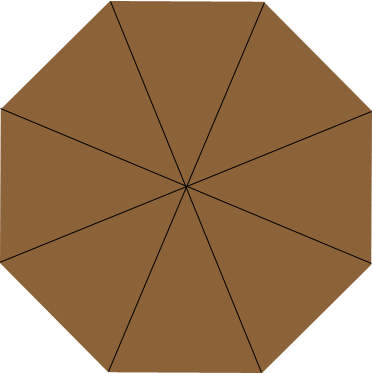
However the joinery in the frame below will be tricky. This might be better as a veneer pattern!

If you want a simple design for the frame underneath you want to keep the cuts few and symmetric. About the simplest would be in the diagram below.

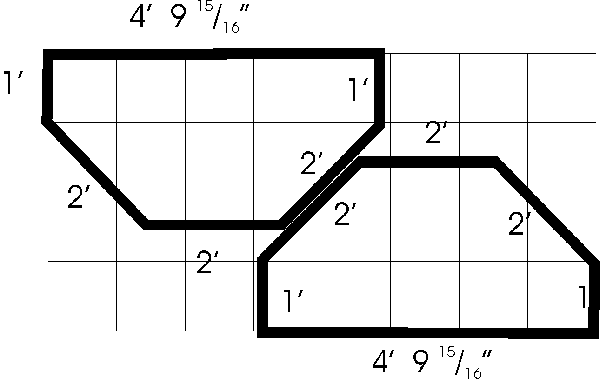
This will also show off a strong but wavy grain (like most oak-surfaced plywood,in which the face veneer is rotary-cut) better than the pattern above will.

Note that the diagonal edges in the middle are each more than an inch away from the center. If you wish to use tongue-and-groove or some other routed edge pattern to make a strong permanent joint, you can easily push the top piece down and/or the bottom piece up to give a little extra wood along the long edge for jointing.

On the other hand, if storage is a problem, this design would work well for a tabletop that disassembles into two halves, with folding legs and an unglued lap joint.

Good luck!
RD

Corey wrote back

This is perfect, but I have one more question. How can you insure that the angles are all identical so that the octagon is symmetrical?

Corey,

If you are making RD's first design then I wouldn't measure angles at all. Mark 2 foot measurements down one side of the sheet and then on the other side 1 foot, 3 measurements of 2 feet and the 1 foot. Join the markings as in the diagram and cut along the lines.

If you are looking at RD's second design then the angle between the 4 feet 9 and 3/4 inch sides and each 1 foot sides is 90 degrees. All the other interior angles are 45 degrees.

Harley