| |||
| Math Central | Quandaries & Queries |
|
Question from Crystal, a student: I'm getting a little confused with this question. At a certain instant, airplane A is flying a level course at 500 mph. At the same time, airplane B is straight above airplane A and flying at the rate of 700 mph. On a course that intercepts A's course at a point C that is 4 miles from B and 2 miles from A. At the instant in question, how fast is the distance between the airplanes decreasing? |
Crystal,
Here is my diagram of what you describe.
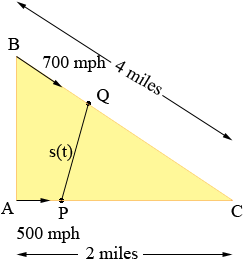
Time t is measured in hours and at time t = 0 hours the airplanes are at A and B. C is the point where their paths meet. At some time t hours later airplane A is at P and airplane B is at Q. Let s(t) be the distance between P and Q. Since A flies at 500 miles per hour the distance from A to P is 500t miles and thus the distance from P to C is 2 - 500t miles. Likewise the distance from Q to C is 4 - 700t miles.
B is directly above A so angle BAC is a right angle and hence cos(angle ACB) = 2/4 = 1/2. Thus the measure of angle ABC is 60o. (My diagram is quite bad!) Thus in triangle QPC you know the lengths of the sides PC and CQ and the measure of the angle between them. Hence you can use the Law of Cosines to write an expression for s(t)2,
s(t)2 = ...
Differentiate both sides of this expression to find
2 s(t) s'(t) = (...)',
evaluate at t = 0 and solve for s'(0).
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.