Dale,

In my diagram B is the centre of the chord, r is the radius of the circle, h is the height of the arc, c is the length of the chord and C is the centre of the circle. Thus |AB| = c/2 and |BC| = r - h.

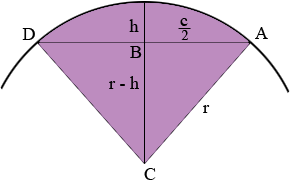
Triangle ABC is a right triangle. Write down Pythagoras theorem for this triangle and solve for r.

The length of the arc AD is given by r θ where θ is the measure of the angle DCA in radians. Since tan(θ/2) = (c/2)/(r - h) you can use your calculator to find θ = 2 tan^-1[(c/2)/(r - h)]. (Make sure you have your calculator on radians not degrees.) Thus the length of the arc is

r θ = 2r tan^-1[(c/2)/(r - h)]

I hope this helps,
Harley