| |||
| Math Central | Quandaries & Queries |
|
Question from Dale: How do I find the central angle if I only have the cord length and radius. |
Hi Dale,
What you have is an isosceles triangle and you know the lengths of the three sides. Join the vertex C to the midpoint M of the base.
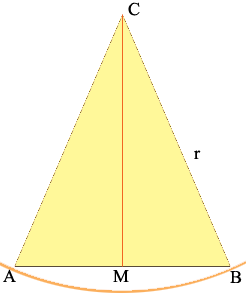
If the radius is r and the length of the chord is c then triangle CMB is a right triangle with |BC| = r and |MB| = c/2. Hence the sine of the angle BCM is (c/2)/r = c/(2r). Hence the central angle BCA has measure
2 sin-1[c/(2r)]
I hope this helps,
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.